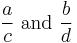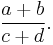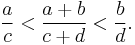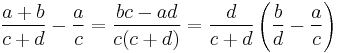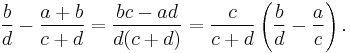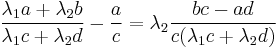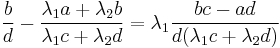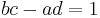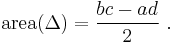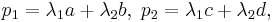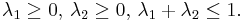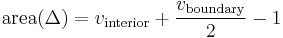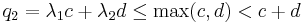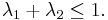Mediant (mathematics)

For mediant in music, see mediant. "Mediant" should not be confused with median.

In mathematics, the mediant (sometimes called freshman sum) of two fractions

$\frac {a} {c} \text{ and } \frac {b} {d}$

$\frac {a %2B b} {c %2Bd}.$

that is to say, the numerator and denominator of the mediant are the sums of the numerators and denominators of the given fractions, respectively.

In general, this is an operation on fractions rather than on rational numbers. That is to say, for two rational numbers q₁, q₂, the value of the mediant depends on how the rational numbers are expressed using integer pairs.

A way around this, where required, is to specify that both rationals are to be represented as fractions in their lowest terms (with c > 0, d > 0). With such a restriction, mediant becomes a well-defined binary operation on rationals.

The Stern-Brocot tree provides an enumeration of all positive rational numbers, in lowest terms, obtained purely by iterative computation of the mediant according to a simple algorithm.

Properties

The mediant inequality: An important property (also explaining its name) of the mediant is that it lies strictly between the two fractions of which it is the mediant: If 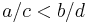$a/c < b/d$ , then

$\frac a c < \frac{a%2Bb}{c%2Bd} < \frac b d.$

This property follows from the two relations

$\frac{a%2Bb}{c%2Bd}-\frac a c={{bc-ad}\over{c(c%2Bd)}} ={d\over{c%2Bd}}\left( \frac{b}{d}-\frac a c \right)$

and

$\frac b d-\frac{a%2Bb}{c%2Bd}={{bc-ad}\over{d(c%2Bd)}} ={c\over{c%2Bd}}\left( \frac{b}{d}-\frac a c \right).$

Assume that the pair of fractions a/c and b/d satisfies the determinant relation 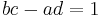$bc-ad=1$ . Then the mediant has the property that it is the simplest fraction in the interval (a/c, b/d), in the sense of being the fraction with the smallest denominator. More precisely, if the fraction 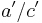$a'/c'$ with positive denominator c' lies (strictly) between a/c and b/d, then its numerator resp. 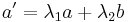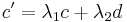denominator can be written as $\,a'=\lambda_1 a%2B\lambda_2 b$ and $\,c'=\lambda_1 c%2B\lambda_2 d$ with two positive real (in fact rational) numbers 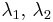$\lambda_1,\,\lambda_2$ . To see why the 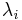$\lambda_i$ must be positive note that

$\frac{\lambda_1 a%2B\lambda_2 b}{\lambda_1 c%2B\lambda_2 d }-\frac a c=\lambda_2 {{bc-ad}\over{c(\lambda_1 c%2B\lambda_2 d)}}$

and

$\frac b d-\frac{\lambda_1 a%2B\lambda_2 b}{\lambda_1 c%2B\lambda_2 d }=\lambda_1 {{bc-ad}\over{d(\lambda_1 c%2B\lambda_2 d )}}$

must be positive. The determinant relation

$bc-ad=1 \,$

then implies that both 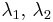$\lambda_1,\,\lambda_2$ must be integers, solving the system of linear equations

$\, a'=\lambda_1 a%2B\lambda_2 b$

$\, c'=\lambda_1 c%2B\lambda_2 d$

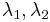for $\lambda_1,\lambda_2$ . Therefore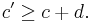 $c'\ge c%2Bd.$

The converse is also true: assume that the pair of reduced fractions a/c < b/d has the property that the reduced fraction with smallest denominator lying in the interval (a/c, b/d) is equal to the mediant of the two fractions. Then the determinant relation bc − ad = 1 holds. This fact may be deduced e.g. with the help of Pick's theorem which expresses the area of a plane triangle whose vertices have integer coordinates in terms of the number v_interior of lattice points (strictly) inside the triangle and the number v_boundary of lattice points on the boundary of the triangle. Consider the triangle 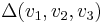$\Delta(v_1,v_2,v_3)$ with the three vertices v₁ = (0, 0), v₂ = (a, c), v₃ = (b, d). Its area is equal to

$\text{area}(\Delta)={{bc-ad}\over 2} \ .$

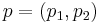A point $p=(p_1,p_2)$ inside the triangle can be parametrized as

$p_1=\lambda_1 a%2B\lambda_2 b,\; p_2=\lambda_1 c%2B\lambda_2 d,$

where

$\lambda_1\ge 0,\,\lambda_2 \ge 0, \,\lambda_1%2B\lambda_2 \le 1. \,$

The Pick formula

$\text{area}(\Delta)=v_\mathrm{interior}%2B{v_\mathrm{boundary}\over 2}-1$

now implies that there must be a lattice point q = (q₁, q₂) lying inside the triangle different from the three vertices if bc −&nsbp;ad >1 (then the area of the triangle is 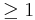$\ge 1$ ). The corresponding fraction q₁/q₂ lies (strictly) between the given (by assumption reduced) fractions and has denominator

$q_2=\lambda_1c%2B\lambda_2d \le \max(c,d)<c%2Bd$

$\lambda_1%2B\lambda_2 \le 1. \,$

Relatedly, if p/q and r/s are reduced fractions on the unit interval such that |ps − rq| = 1 (so that they are adjacent elements of a row of the Farey sequence) then

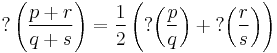
$?\left(\frac{p%2Br}{q%2Bs}\right) = \frac12 \left(?\bigg(\frac pq\bigg) %2B {}?\bigg(\frac rs\bigg)\right)$

where ? is Minkowski's question mark function.

In fact, mediants commonly occur in the study of continued fractions and in particular, Farey fractions. The nth Farey sequence F_n is defined as the (ordered with respect to magnitude) sequence of reduced fractions a/b (with coprime a, b) such that b ≤ n. If two fractions a/c < b/d are adjacent (neighbouring) fractions in a segment of F_n then the determinant relation 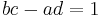$bc-ad=1$ mentioned above is generally valid and therefore the mediant is the simplest fraction in the interval (a/c, b/d), in the sense of being the fraction with the smallest denominator. Thus the mediant will then (first) appear in the (c + d)th Farey sequence and is the "next" fraction which is inserted in any Farey sequence between a/c and b/d. This gives the rule how the Farey sequences F_n are successively built up with increasing n.

Mediant (mathematics)

Properties

External links